INSTITUTE FOR NUCLEAR THEORY
News
Home | Contact | Search | News archive | Site Map

|
INSTITUTE FOR NUCLEAR THEORY News
Home | Contact | Search | News archive | Site Map |
|||||
Simulations and Symmetries: Cold Atoms, QCD, and
Few-hadron Systems
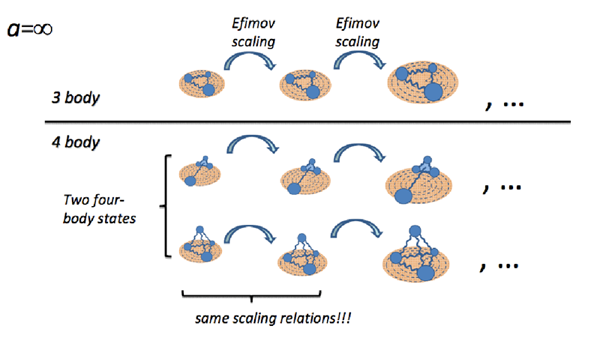
Rapid advances in the experimental study of systems of cold atoms have provided controlled environments in which to explore quantum many-body dynamics. In particular, the ability to trap atoms, and dictate the strength of their interaction through Feshbach resonances, has provided a laboratory with which to investigate the consequences of varying scattering lengths all the way from the range of the atom-atom interaction to infinity. When the atom-atom scattering length is infinite the resulting system is "unitary", as atom-atom scattering saturates the bound imposed by the conservation of probability. In this limit the many-body quantum system has scale-invariance for length scales larger than the range of the two-body interaction, and this leads to the existence of "universal" properties, which do not depend on the underlying force. A famous example of the implications of a unitary atom-atom interaction is found in the spectrum of particular three-atom systems. As predicted by Efimov long ago, the spectrum of such systems has states that are simply scaled copies of each other with energies that are multiplicatively related. This is now understood in the language of the renormalization group as resulting from an infrared limit-cycle. In the last few years it has further been discovered that the underlying scaling symmetry impacts the structure of systems composed of more than three bodies, as illustrated in Figure 1. Figure 1. Four-body Efimov states built upon three-body Efimov states. [Image taken from C. Greene's program presentation "Universality and the Efimov effect".]
The relation between systems near unitarity and nuclear physics is that the parameters of quantum chromodynamics (QCD) are such that the s-wave nucleon-nucleon interaction produces scattering lengths that are much larger than the range of the interaction. The triton is then "close" to having a second state, which would be identified as an Efimov state, and it has been conjectured that light-quark masses would need to change only slightly from their values in nature to produce this Efimov state. Lattice QCD is the calculational tool with which this could be definitively explored, but, presently, the only practical tool available to map out the light-quark mass dependence of nuclear processes is effective field theory (EFT). To be reliable such an EFT has to build in the fine-tuning inherent in the nucleon-nucleon scattering lengths, and the role of the important low-energy scales of QCD.
Systems near Unitarity
Meanwhile, the last few years saw the first theoretical predictions for four-body loss features in cold atomic gases at or near unitarity. These have recently been validated in experiments by groups at Innsbruck and Rice Universities. This confirms that a four-body interaction is not required to define a four-body system of bosons interacting via short-range forces alone. New universal predictions for that system, such as those shown in Figure 1, are the result. Comparisons between such predictions for the four-body system and experimental measurements in the controlled environment of a cold atomic gas are ongoing, and promise to reveal much about four-particle quantum dynamics.
From QCD to light nuclei, via modern nuclear interactions
"Halo" nuclei such as Helium-6 and Helium-8 are a particular challenge in this last regard, since the final few neutrons in these systems are bound by much less than the average binding energy per nucleon in typical nuclei. Ab initio calculations are overcoming the challenges, and making important progress towards quantitative description of these systems. Good agreement is now found with the very precise charge-radius numbers obtained from laser spectroscopy of Helium-6 and Helium-8 atoms (see Figure 2). Figure 2. Artist's impressions of neutron distribution (blue) and proton distribution (red), as well as measured charge radii, for Helium-4, Helium-6, and Helium-8 isotopes. [Image taken from P. Mueller's program presentation, "Laser trapping and probing of exotic Helium isotopes".]
Halo nuclei are fascinating systems partly because they provide another connection to physics near unitarity. Similarities and differences between the s-wave few-body systems near unitarity discussed above and systems with resonant p-wave cluster-neutron interactions (e.g. Helium-6 and Helium-8) are under investigation, with a particular focus on whether the latter display "universal properties" similar to those found in systems with resonant s-wave interactions.
Nuclear Physics from Lattice QCD
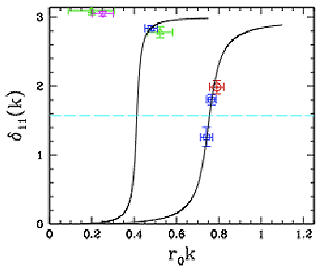
What would seem to be a straightforward task for lattice QCD is the calculation of the nucleon-pion scattering phase-shift in the Delta-isobar region, and the subsequent identification of the pole and width of the Delta (analogously, similar calculations for other unstable hadrons such as the rho meson, as shown in Figure 3). The recent work by the QCDSF collaboration makes clear the extent of the difficulties of such calculations, and that calculations in big enough volumes will require significantly larger computational resources than have been used to date. Figure 3. The π π phase shift versus pion
momentum in the vicinity of the ρ-resonance. The right curve corresponds to a π mass of 250 MeV, while the left one if for a π mass of 390 MeV. [QCDSF collaboration, PoS LATTICE2008: 136,2008, e-Print: arXiv:0810.5337 [hep-lat].]
This is just one example where knowing the expected energy-spectrum of few-hadron systems placed in finite volumes is key to developing an understanding of what we can expect in future lattice QCD calculations. It is anticipated that the spectrum beyond the nuclear ground state is quite complicated, and so predictions for the spectrum based upon a reliable EFT and modern few-nucleon methods would be very valuable. The usefulness and practicality of different boundary conditions for both Lattice QCD and nuclear many-body calculations are also being thoroughly investigated (as illustrated in Figure 4). The ability to benchmark finite-volume effects using data from trapped atomic systems is very beneficial here.
Figure 4. Theoretical and experimental boundary conditions that are imposed upon few-nucleon systems. Lattice QCD calculations are presently restricted to (hyper-)cubic volumes with periodic boundary-conditions, while nuclear many-body calculations and atomic experiments use harmonic oscillator potentials. [Image taken from T. Luu's program presentation "Nuclear Physics within Finite Volumes".]
Continued collaboration between lattice QCD and few-body physics is essential in order to optimally determine the consequences of QCD for nuclear physics.
(INT program March 15 - May 21, 2010)
Reported by: Daniel Phillips (Ohio U),
Hans-Werner Hammer (U Bonn), and Martin Savage (U Washington)
Date posted August 9, 2010
![]()
A rapidly evolving experimental program is directed at understanding atomic systems with scattering lengths that are tuned to be large compared to the range of the underlying force. Physical chemists, atomic theorists and nuclear physicists employ a variety of theoretical formalisms to try and understand such systems. These include the direct solution of the Schrodinger equation, evaluation of the path-integral using large computational resources, together with lattice and Monte Carlo methods and Effective Field Theory (EFT) techniques. It is encouraging to find that in many instances where the precision of such calculations is high, agreement is found between the different theoretical approaches. A compilation of such results can be found at https://lore.phys.washington.edu/coldatoms/index.php/Main_Page. Especially notable is the ongoing effort to calculate the "Bertsch Parameter", which is the dimensionless constant that relates the energy of a system of particles at unitarity to that of a free Fermi gas at the same density. The field is converging on a value for this important parameter through the use of several different experimental and theoretical techniques.
The last two decades have seen remarkable progress toward understanding the manner in which the approximate chiral symmetry of QCD impacts nuclear forces, and also in the use of the resulting forces to describe the structure and reactions of light nuclei. Although several formal issues regarding the chiral expansion of nucleon-nucleon and multi-nucleon interactions remain unresolved, nuclear forces based on this approach have achieved considerable phenomenological success. The expansion is now used to produce accurate calculations of the low-energy interactions of pions and photons with light nuclei, and impressive results for nuclear structure are achieved in ab initio nuclear many-body calculations that take these modern nuclear forces as input.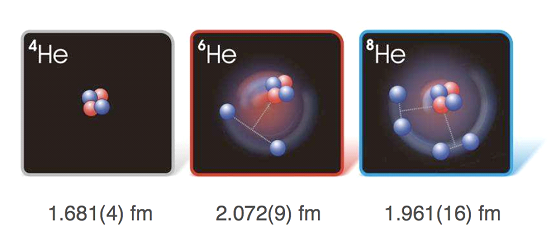
Lattice QCD is coming of age, with computational resources and algorithm development now on track to allow for the calculation of the properties and interactions of the lightest nuclei within a decade. The techniques required to extract nuclear interaction parameters from lattice QCD calculations are well established in the two-hadron sector, and they (Luscher's method) are currently being used to extract low-energy elastic scattering phase shifts. An understanding of the calculations that should be performed, and their translation into break-up amplitudes, for inelastic processes, requires further developments.